No, It's Not All The Same
My friend, your book premise is horribly whack, but good news: the details can stay the same as long as the reader understands that this is only Step One

Recently I was asked to review a book on functional programming for a friend.
I love functional programming, I love all programming really, so I was happy to give it a shot, but I had a hunch from reading his tweets that he was heading down the wrong road.
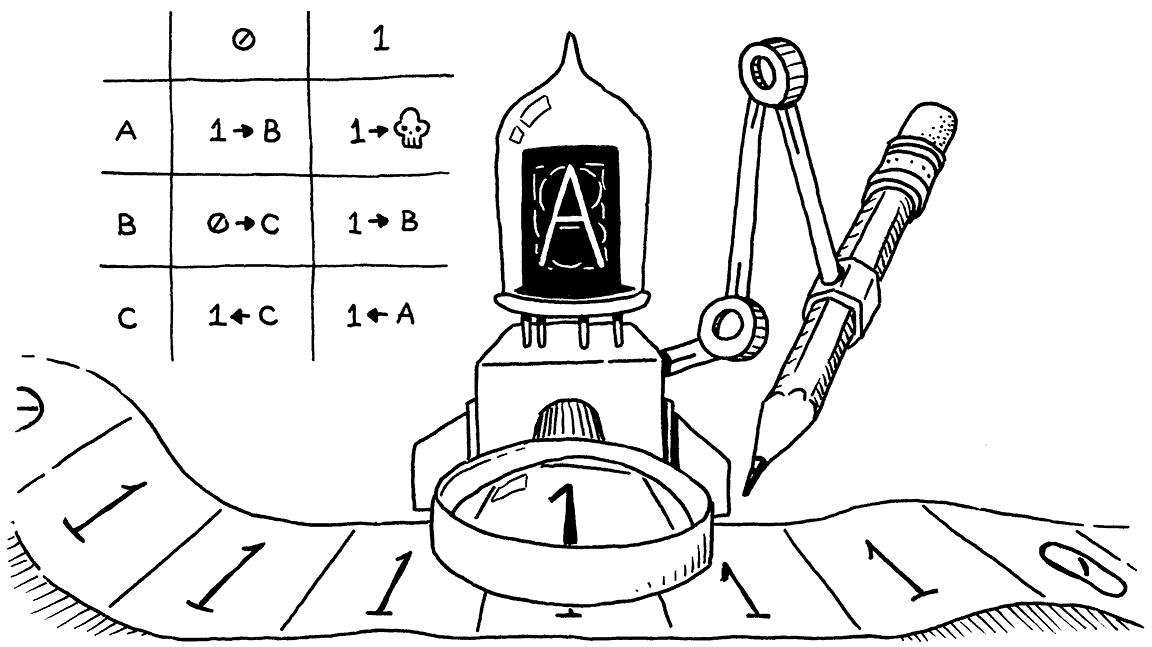
My friend's preface contains this (after a few paragraphs about the history of computing):
"...Turing’s invention was the forebear of all modern digital computers. Every digital computer is, for all intents and purposes, a Turing machine. Every program that has ever executed on a digital computer is, for all intents and purposes, a Turing Machine program.
Church and Turing later collaborated to show that Turing’s and Church’s approaches were equivalent. That every program in a Turing machine can be represented in Predicate Calculus, and vice versa. Functional Programming is, for all intents and purposes, programming in predicate calculus.
So these two styles of programming are equivalent in a mathematical sense. What we are going to examine in this book is not that equivalence; but rather the ways that using the functional approach affects the structure and design of our programs. We will seek to determine whether those differences structures and designs are in any sense superior, or inferior, to those that arise from use the Turing approach..."
My translation while reading: Church = Turing = Programming so it's all the same. They're all programming so Pure Functional Programming (FP) is just a matter of learning new ways to say the same old stuff.
You see the sleight of hand here, right? We begin with history, move to independent yet similar mathematical discoveries, then conclude that all programming is equivalent. Finally, we propose that we will see whether some structures or better or worse than others.
There's no programmer here. Programmers matter as much as any other part of any symbolic system, as we discussed in the previous essay.
His premise reduces to "math is math", which is true yet completely useless to a practicing programmer. In addition, given this premise, the book can only make one of two conclusions, nothing matters, or "math is math", or things matter but it's outside the scope of the book, i.e. it's a matter of taste. The second is a "pick whatever works for you better", conclusion which only brings the poor programmer back into the discussion to use as a deus ex machina and foil for any useful advice to be given, e.g. how would taste actually be relevant here, why, and how would one judge between different tastes? All the really good questions are left as scraps for the reader to gather up after the meal and to try to make something palatable.

The practice of programming is about people solving problems for other people. Math is a lens for that, but not the only one.
Reducing it all to math is like saying "The main difference between Lisp and Java is the use of parenthesis or braces."
This is true, but the truth is reduced to the point of being circular. The writer is confusing the inductive mechanics of what happens under the hood as you program with the abductive and deductive act of programming itself.
My goal is to point this out without my friend diving back into "it's all math". We coders love to be reductionist when it suits us.
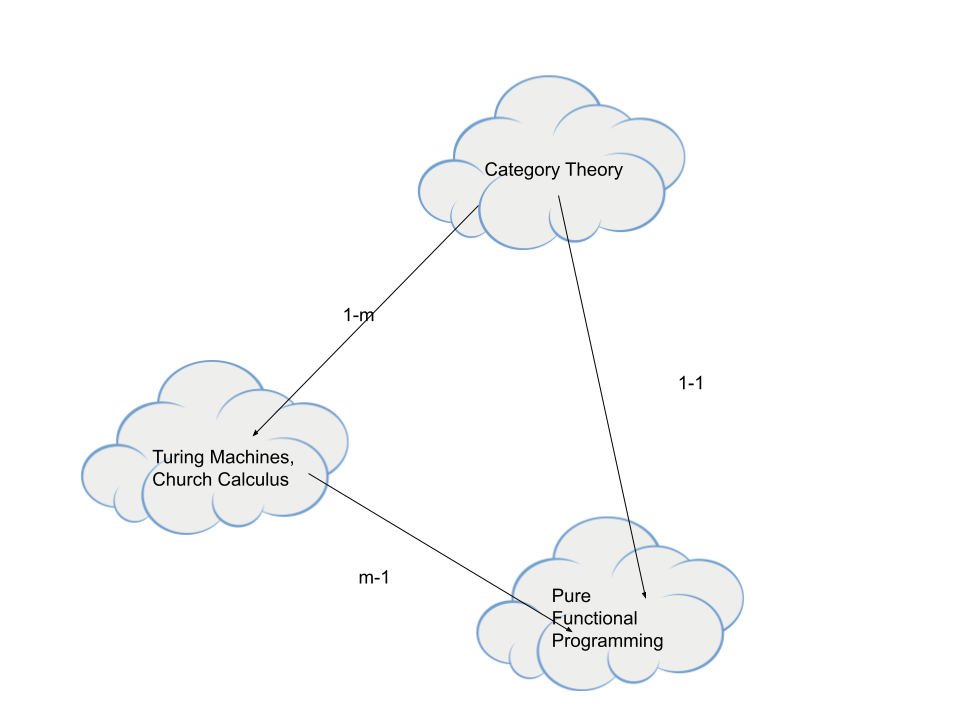
Let's try this a different way. What would most folks think of as being the ultimate programming language? Probably Haskell. Why is that? Because Haskell attempts to directly map programming to Category Theory, which is the basis of large hunks of math, of which Turing Machines are just one. Let's look at the human part of this visually.
It's not unusual to read on tech news that something-or-another has been found to be "Turing Complete", i.e. capable of universal computation. Why is that? Nobody ever announces the discovery of a new integer. Wikipedia defines Turing Complete as
"...Turing completeness is significant in that every real-world design for a computing device can be simulated by a universal Turing machine. The Church-Turing thesis states that this is a law of mathematics - that a universal Turing machine can, in principle, perform any calculation that any other programmable computer can..."
So why would discovering something in tech being Turing Complete be any kind of surprise? Because it's all, any kind of modern technology, Turing Complete, right? It seems trite.
It's because of the ability and manner of which actual people use it. In some technologies, an actual human has the ability to manipulate some underlying symbology in a way that's Turing Complete. In others, people are locked out of all or part of that ability. Your Roomba isn't Turing Complete, but given the right hardware access, it can be. (And, of course, it's Turing Complete to somebody. All tech has to be.)
The people part matters.
Turing talked about tape and sequential operations. Church was working with predicate calculus. This is much the same as the difference in "math" as a universal set of self-consistent axioms, i.e. parallel lines never meet, the interior angles of a triangle add to 180 degrees, and so forth, and math as a series of steps, "To do long division, first you ..." They're both describing the same thing, but one is a "why" and the other is a "how."
Some folks code using symbols from Church Encoding, i.e. Lambda Calculus (LC). That's a notational issue. There are some really cool reasons why programming languages end up using LC, that's because it maps back to CT, the grandfather. But don't confuse symbols in a language with LC or CT (unless you know that the language is constructed to be very strict. Most of the time such language features are much more like selling points than axioms.)
So there are a bunch of different things you can find lying around, or create, that implement the subset of Category Theory such that they are Turing Complete. There is something you can do with these things in order to implement sequential operations that will provide universal computation. The tape has to have a reader, the code has to have a sequencer (the compiler usually). It's a "how", or a list of mechanical things to do in order to do something else.
Because Category Theory is a "why" area, it has the smallest possible building blocks imaginable to do lots of things, including programming. There is no reader. It's fixed rules with relationships. These things relate and transform to these other things in any order or sequence. Why? Because a person has said that these types transform to these other types. CT and the grandkid FP are both declarative. It's semiotics and deduction. You describe and declare it, you are done. (From an analysis standpoint.) Other programming is procedural. You're telling the computer to do some stuff in some kind of order.
Any real-world programming problem can be broken down into a minimal amount of Category Theory symbology. From that point, it is impossible to reduce it further. Just like Turing had a minimum number of "what to do", operations, that described all of computing, CT has a minimum number of "what relates to what" relations that describe not only computing, but big hunks of math as well.
Category can give you minimum solutions, but very importantly, the same is not true the other way! For any given real-world problem, there's an infinite amount of complexity one can add trying to solve it no matter which paradigm you use. Therefore, pure functional programming, using any kind of language that supports it, should naturally strive towards minimum symbology. Otherwise you're just making the complex mess you already had even more impenetrable by solving things a different way.
I'm a big fan of "lift and shift" learning functional programming, taking what you know from one paradigm and directly translating it into another programming paradigm if you can, but that's only Step One of learning that new paradigm. You can't stop there. You can't say that it's all the same and allow people to stop and feel like they've done anything useful. Even worse, if you imply that mixed mode problem-solving is just as good as one or the other? When you do these kinds of things, you're hurting the development community by inflicting your ignorance out on the masses. Stop doing that.[1] There's an old joke that all programming is just ones and zeros. All you have to do is just get them in the correct order! But that's a joke. Your programming career should not consist of reducing important differences to the point that you make a joke out of your work. You're better than that.
Good news, my friend, the details of your lift-and-shift premise work as part of a larger learning program, but only if you give up your "everything is the same" premise and move to a "you need to change the way you solve problems" beginning of your book.
- I could have also argued this from a pure theory standpoint, without bringing the programmer into the equation, but taking a hard look at the Curry-Howard Correspondence. I actually prefer this line of argument, since from there we directly lead into how science and knowledge happens, but it's both deep and not necessary. The concept of pure functional coding naturally being a minimalist approach is far more helpful to the average coder, and something they can apply right away, than a deep dive into history or theory.

Comments ()